| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- django httpd error
- 2661 java
- django settings.py
- windows 원격 연결 설정
- 2961 도영이가 만든 맛있는 음식
- 18233 러버덕
- 18233 java
- django
- 1188 java
- 2961 java
- java di
- 1188 음식 평론가
- 2643 java
- 공유기 원격 설정
- The requested operation has failed!
- 18233 비트마스킹
- Problems occurred while performing provisioning operation
- django 웹 페이지
- 14711 타일 뒤집기
- windows apache wsgi 에러
- django 프로젝트 시작
- apache pythonpath
- 2643 색종이 올려 놓기
- APPEND_SLASH = FALSE
- 원격 연결 포트 포워딩
- django The requested operation has failed!
- django windows 배포 에러
- 14711 java
- 2661 좋은 수열
- django apache deploy error
라이브러리는 도서관 아닌가요
백준(BOJ) 2133 타일 채우기 java 본문
https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
문제가 아주 심플하다.
Q) 3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
아래 그림은 3×12 벽을 타일로 채운 예시이다.
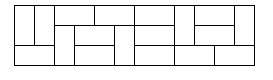
하지만 풀이에 대한 구상은 간단하지 않다.
N이 홀수일 때는 모두 0이다.
N이 짝수일 때를 생각해봐야 하는데, 규칙을 찾기 위해 4개까지는 그리면서 해볼만 하다.
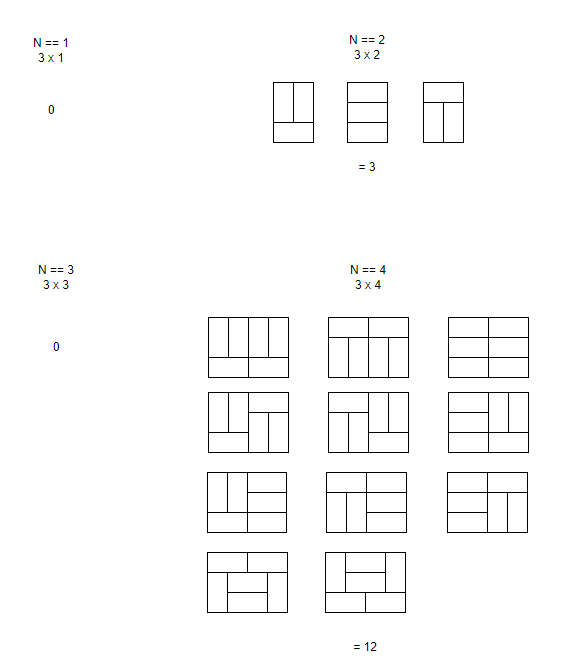
문제는, N이 6 이상일 때부터인데,
일단 결론은 N==6일 때 41개이다. ( 33 + 6 + 2 )
우선 항상 특이 케이스 2개짜리가 발생한다는 점을 눈여겨봐야 한다.
(N=4일 때의 특이 케이스)
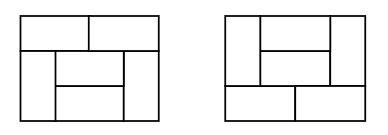
(N=6일 때의 특이 케이스)

이러한 특이 케이스는 기존의 N=2일 때의 모양들로 구성할 수 없는 새로운 유형이다.
특이 케이스를 제외하고는 N=2일 때의 조합이 기초가 된다는 점을 유의하자.
다시 N=6일 때로 돌아와서, 우리는 일반화하기 위해서 아래와 같이 생각할 필요가 있다.
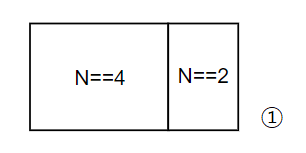

N=4일 때와 N=2일 때의 조합으로 N=6일 때를 구성할 수 있다. (그리고 나중에 특수 케이스 2개를 더하면 된다.)
홀수로 구성할 수 있는 경우는 없기 때문에 결국 기존의 짝수 조합으로 새로운 조합을 만들 수 있다는 점이 중요하다.
① (N=4) x (N=2) 는 11 x 3 = 33이 된다.
② (N=2) x (N=4) 는 3 x 2 = 6이 된다.
왜 두번째 경우에서 (N=4)는 2가 되었는지 의문이 생길 것이다.
이는 중복을 피하기 위해 이전 N=4일 때 나온 특이 케이스만을 곱한 것이다.
N=2로 구성할 수 있는 N=4를 만들어 N=6으로 구성하기 시작하면 첫번째 경우 (N=4) x (N=2)와 겹치기 시작한다.
그래서 모두 더하면 33 + 6 + 2 = 41이 되는 것이다.
마지막으로 N=8일 때를 계산해보자. (빨간색은 특이 케이스만을 의미한다.)
경우 1: 3x6 + 3x2 크기로 채운다.
→ (N=6) x (N=2) = 41 x 3 = 123
경우 2: 3x8크기의 타일을 3x4 + 3x4 크기로 채운다.
→ (N=4) x (N=4) = 11 x 2 = 22
경우 3: 3x8크기의 타일을 3x2 + 3x6 크기로 채운다.
→ (N=2) x (N=6) = 3 x 2 = 6
경우 4: 새로 발생하는 특이 케이스 2개
→ 2
123 + 22 + 6 + 2 = 153
그래서 우리는 N=10의 계산 방식이 아마도 아래와 같다고 짐작하게 된다.
경우 1: ...
→ (N=8) x (N=2)
경우 2: ...
→ (N=6) x (N=4)
경우 3: ...
→ (N=4) x (N=6)
경우 4: ...
→ (N=4) x (N=8)
경우 5: 새로 발생하는 특이 케이스 2개
→ 2
빨간색은 모두 2로 치환된다. (앞의 특이 케이스들이니까)
... 그래서 다시 N=8로 돌아와 식을 뽑아내보면 아래와 같다.
C(8) = { C(6) x C(2) } + { C(4) x 2 } + { C(2) x 2 } + { 2 }
좀 더 일반화하기 위해 아래와 같이 바꿔주자. [ N(0)은 1 ]
C(8) = { C(6) x C(2) } + { C(4) x 2 } + { C(2) x 2 } + { C(0) x 2 }
마지막으로 점화식을 완성하면,
C(N) = C(N-2) x C(2) + C(N-4) x 2 + C(N-6) x 2 + ... + C(N-2) x 2 + C(0) x 2
위의 식에서 코드로 풀어내기 위한 특징을 뽑아보자.
C(N) = C(N-2) x C(2) + C(N-4) x 2 + C(N-6) x 2 + ... + C(N-2) x 2 + C(0) x 2
위와 같은 식이 만들어진다.
파랗게 칠해진 부분은 1중 for문에서 먼저 계산을 해야 한다.
뒤의 2가 연달아 곱해지는 부분은 2중 for문에서 해결할 것이다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
// N == 홀수
if(N%2 == 1){
System.out.print(0);
return;
}
// 각 길이에 대한 dp 배열
int[] dp = new int[N+1];
dp[0] = 1; // 사실 0이란 경우는 없다. 그냥 기초항.
dp[1] = 0;
dp[2] = 3;
for(int i=4; i<=N; i+=2){
dp[i] = dp[i-2] * dp[2];
for(int j=i-4; j>=0; j-=2){
dp[i] += dp[j] * 2;
}
}
System.out.print(dp[N]);
}
}'알고리즘 문제' 카테고리의 다른 글
| 백준 (BOJ) 15810 풍선 공장 java (0) | 2022.04.05 |
|---|---|
| 백준 (BOJ) 10815 숫자 카드 java (0) | 2022.03.25 |
| 백준(BOJ) 1025 제곱수 찾기 java (0) | 2022.03.18 |
| 백준(BOJ) 1991 트리 순회 java (0) | 2022.03.15 |
| 백준 (BOJ) 16236 아기 상어 java (0) | 2021.12.12 |
