| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 2661 좋은 수열
- 18233 java
- 2643 java
- 공유기 원격 설정
- windows apache wsgi 에러
- 2961 도영이가 만든 맛있는 음식
- 원격 연결 포트 포워딩
- django
- APPEND_SLASH = FALSE
- windows 원격 연결 설정
- 2661 java
- django windows 배포 에러
- django apache deploy error
- 14711 java
- 2643 색종이 올려 놓기
- The requested operation has failed!
- 18233 비트마스킹
- django settings.py
- django 웹 페이지
- django The requested operation has failed!
- 2961 java
- 18233 러버덕
- 1188 음식 평론가
- django httpd error
- 1188 java
- java di
- django 프로젝트 시작
- 14711 타일 뒤집기
- apache pythonpath
- Problems occurred while performing provisioning operation
라이브러리는 도서관 아닌가요
백준 1188 음식 평론가 java (greedy, gcd) 본문
https://www.acmicpc.net/problem/1188
1188번: 음식 평론가
첫째 줄에 소시지의 수 N과 평론가의 수 M이 주어진다. (1 ≤ N, M ≤ 100)
www.acmicpc.net
문제는 쉽게 이해가 가는데 풀이가 쉽게 안 나오는 문제.
가장 먼저 소시지를 자르는 횟수에 대해 얘기해보자.
소시지 하나를,
3조각 만들려면 2번 자른다.
4조각 만들려면 3번 자른다.
5조각 만들려면 4번 자른다. --> (목표 조각-1) == 자를 횟수
그 다음으로 왜 최대 공약수를 구하는지부터 의문이 생길 수 있다.
중요한 부분은 '알맞은 비율로' 소시지를 잘 나눠서 잘라줘야 한다는 점이다.
이 비율을 구하기 위해서 생각을 해볼 필요가 있다.
먼저 예를 들어서, 4개의 소시지를 6명에게 나눠주는 문제는 사실
2개의 소시지를 3명에게 나눠주는 것과 그 궤를 같이 한다.
편의상 이렇게 표현하자. (4, 6) --> 2(2, 3)
(2, 3)과 같은 방식을 *2번 더 반복하면 되는 것이다.
실제로 (2, 3)은 2번, (4, 6)은 4번 잘라주면 된다.
이때 최대공약수(GCD)가 왜 나오는지 대략 감은 온다.
자 그럼 좀 더 세부적인 문제로 들어가서,
2개의 소시지를 3명에게 나누어주려면 얼마나 잘라야 하나?
비율적으로 2/3씩 나눠가진다. 즉 근사치로 0.66666...만큼 나눠가지면 된다는 것을 안다.
첫번째 소시지를 1/3만큼 잘라주고, 두번째 소시지도 1/3만큼 잘라주면,
2/3, 2/3, 2/3만큼씩 가지게 된다.
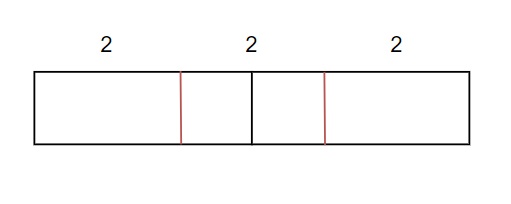
하나의 소시지처럼 이어붙이면 위의 이미지처럼 된다.
결론적으로 하나로 이어붙인 두 소시지를 1/3씩 잘라주면 그것이 답이 된다.
다르게 말해서 저 이어붙인 소시지를 1/3씩 3조각으로 나누기 위해서는 몇번 더 칼을 대야 할까?
당연히 답은 두 번이다.
아직 좀 멀었다. 다른 예를 하나 더 들어보자.
n=3, m=6이라고 할 때,
소시지 3개를 6명이서 나눠 가지려면 각 소시지를 1/2씩 6명이 나눠가져야 한다.
3개를 한줄로 놓고, 하나의 1/2에 해당하는, 다시 말해 하나에 대한 2조각의 크기 만큼씩 잘라서 나눠가진다.
즉 한 번 자른다.
세번 반복해서(gcd=3) 각 1/2 사이즈를 6개 만드므로 답은 3이다.
또 다른 예로, 위의 n=3, m=6을 3(1,2)로 묶어낼 수 있고,
세부 문제로 들어가서 (1, 2)을 보면 당연히 한 소시지를 2조각으로 나눠가지게 되고 답은 한번만 자르면 된다.
깔끔하게 정리하고 사례를 좀 더 추가해서 보자
n=1, m=2 → gcd=1이 되고, 2는 소시지 하나에 대한 목표 조각 수가 된다.
n=3, m=6 → gcd=3가 되고, 2는 소시지 하나에 대한 목표 조각 수가 된다.
n=4, m=6 → gcd=2가 되고, 3은 소시지 하나에 대한 목표 조각 수가 된다.
n=3, m=9 → gcd=3이 되고, 3은 소시지 하나에 대한 목표 조각 수가 된다.
n=2, m=3 → gcd=1이 되고, 3은 소시지 하나에 대한 목표 조각 수가 된다.
...
** 마지막 부분을 살펴보면,
n=2, m=3 → gcd=1이 되고, 3은 소시지 하나에 대한 목표 조각 수가 된다...고 했는데,
1개당 3조각으로 나누면 한 사람당 비율적으로 2조각씩 나눠가질 수 있게 된다.
하지만 실제로 하나를 3조각을 만드는 게 아니다. 비율적으로 가질 목표 조각 수에 대한 이야기일 뿐,
실제로 자르기 위한 횟수를 아직 구하지 않았다.
( 또한 gcd와 목표 조각 수를 곱해봐야 아직 답 안 나온다. 목표 조각 수일 뿐 잘라야 하는 횟수가 아니기 때문 )
이런 사례를 적어놓고 계속 살펴보면,
(총 사람 수 / gcd) 가 하나의 소시지에 대한 목표 조각 수라는 규칙성이 성립한다는 것을 알 수 있다. 하 눈 아프다.
다시 써보자.
n=1, m=2 → gcd=1이 되고, 2=(2/1)는 소시지 하나에 대한 목표 조각 수가 된다.
n=3, m=6 → gcd=3가 되고, 2=(6/3)는 소시지 하나에 대한 목표 조각 수가 된다.
n=4, m=6 → gcd=2가 되고, 3=(6/2)는 소시지 하나에 대한 목표 조각 수가 된다.
n=3, m=9 → gcd=3이 되고, 3=(9/3)는 소시지 하나에 대한 목표 조각 수가 된다.
n=2, m=3 → gcd=1이 되고, 3=(3/1)는 소시지 하나에 대한 목표 조각 수가 된다.
아직도 목표 조각 수일 뿐 자를 횟수를 구하지 않았다.
그럼 이제 제일 앞에서 말했던, (목표 조각 수-1) == 자를 횟수와 같이 엮어서 생각하면 로직을 뽑아낼 수 있다.
목표 조각 수에 하나를 뺀 값이 잘라야 하는 횟수이기 때문에,
gcd(n,m) * ( m/gcd(n,m) - 1 ) → 정답
( m/gcd(n,m) - 1 )에 gcd(n,m)을 곱해주는 이유는,
해당 값이 오로지 하나의 소시지에 대해 나눠가져야 하는 조각 수이기 때문이다.
gcd의 값만큼 곱해주어야 모든 소시지에 적용이 된다는 뜻이다.
또한 다르게 접근해서 위에서 살펴봤다시피
4개의 소시지를 6명에게 나눠주는 문제는 사실
2개의 소시지를 3명에게 나눠주는 것과 그 궤를 같이 한다... 라고 했다.
(2,3)에서 해결한 작은 문제의 답을 (4,6)에 해당하는 gcd 값 2만 곱하면, (4,6)의 답이 나오는 것이다.
마지막으로 gcd(n,m) * ( m/gcd(n,m) - 1 ) 를 정리해서 풀어내면,
m - gcd(n,m) 가 된다. 휴
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
// 3조각 만들려면 2번 자른다.
// 4조각 만들려면 3번 자른다.
// 5조각 만들려면 4번 자른다. --> 목표 조각-1 == 자를 횟수
// (m/gcd -1) * gcd == m - gcd
System.out.print(m - gcd(n, m));
}
// gcd(a, b) = gcd(b, r), r is mod value of a, b
static int gcd(int n, int m){
while (m > 0){
int temp = n;
n = m;
m = temp % m;
}
return n;
}
}
'알고리즘 문제' 카테고리의 다른 글
| 백준 14711 타일 뒤집기 java (dp) (2) | 2022.09.25 |
|---|---|
| 백준 2643 색종이 올려놓기 java (dp) (1) | 2022.09.25 |
| 백준 5002 도어맨 java greedy (0) | 2022.09.09 |
| 백준 6068 시간 관리하기 java greedy (0) | 2022.09.08 |
| 백준 (BOJ) 4781 사탕가게 java greedy (0) | 2022.09.08 |
